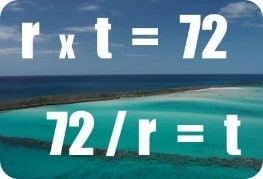I am sure you know the thumb rule of 72. We all use it to know when we can double the money or what rate of returns we ought to earn to double our money. But do you know why 72 is used and not other numbers like 71 or 72?
Well, it depends on the frequency of compounding. If the compounding is done annually (example calculating mutual funds returns across 5 years time horizon), the rule of 72 is best. But in case the compounding is done on a daily basis (your savings account), it is best to use the rule of 69.
The integer 69 or 69.3 to be precise is most appropriate but it is not used since these are not “math-friendly”. It means it is not divisible easily, so the rule of 72 is used for its friendliness.
72 = 2 x 36 or 3 x 24 or 4 x 18 or 6 x 12 or 8 x 9
71 = ???
70 = 2 x 3 or 5 x 14 or 7 x 10
69 = 3 x 23
This is the reason 72 is used most widely.
The simplest way to use Rule of 72 :
We all love to create mental goals and normally the first one is to “how will I reach my first 1 Cr mark”. You can harness rule of 72 for this.
It can help you plan and project your future. Let’s say you’ve saved up Rs 25,00,000, but you want to be a crorepati. You simply need to double your money twice (25 lakh double is 50 lakhs and 50 lakhs double is 1 Cr). With 6% interest, that will take 12 + 12 years, so 24 years. If you can somehow get 12%, you’ll have your billion in 6 + 6 years, so just 12 years. Twice the return earned, half the time killed. Excellent.
Suppose you cannot take the risk and will earn only 6%, then what? If you’re starting with Rs 25,00,000 and also investing Rs 500,000 a year, you can add Rs 5000,000 in ten years, your original Rs 25,00,000 will have nearly doubled, and your earlier annual saving of Rs 500,000 investments will have had time to grow. You can roughly estimate you could be a crorepati within 10 years, even at the 6% rate of return.
Remember these are just approximate calculation and for exact numbers use a compounding calculator. Rule of 72 works best with a steady rate of return.
How precise is Rule of 72?
The below chart calculates the difference between the observations obtained from Rule of 72 and in Actual, at given Rate of Return:

So it works precisely if the Return range is 6% to 18%… Isn’t this what we aim for!
Share with me when and who taught you the rule of 72 first? Was I able to convey an extra bit which will help you? You’re views awaited in the comments section.